One of the more interesting capabilities in Solr's new statistical library is cross-correlation. But before diving into cross-correlation, let's start by describing correlation. Correlation measures the extent that two variables fluctuate together. For example if the rise of stock A typically coincides with a rise in stock B they are positively correlated. If a rise in stock A typically coincides with a fall in stock B they are negatively correlated.
When two variables are highly correlated it may be possible to predict the value of one variable based on the value of the other variable. A technique called simple regression can be used to describe the linear relationship between two variables and provide a prediction formula.
Sometimes there is a time lag in the correlation. For example, if stock A rises and three days later stock B rises then there is a 3 day lag time in the correlation.
We need to account for this lag time before we can perform a regression analysis.
Cross-correlation is a tool for discovering the lag time in correlation between two time series. Once we know the lag time we can account for it in our regression analysis using a technique known as lagged regression.
Working With Sine Waves
This blog will demonstrate cross-correlation using simple sine waves. The same approach can be used on time series waveforms generated from data stored in Solr collections.
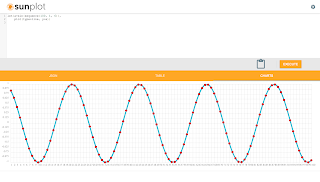
The screenshot below shows how to generate and plot a sine wave:
Let's break down what the expression is doing.
let(a=sin(sequence(100, 1, 6)),
plot(type=line, y=a))
- The let expression is setting the variable a and then calling the plot function.
- Variable a holds the output of the sin function which is wrapped around a sequence function. The sequence function creates a sequence of 100 numbers, starting from 1 with a stride of 6. The sin function wraps the sequence array and converts it to a sine wave by calling the trigonometric sine function on each element in the array.
- The plot function plots a line using the array in variable a as the y axis.
Adding a Second Sine Wave
To demonstrate cross-correlation we'll need to plot a second sine wave and create a lag between the two waveforms.
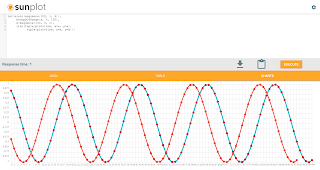
The screenshot below shows the statistical functions for adding and plotting the second sine wave.
Let's explore the statistical expression:
let(a=sin(sequence(100, 1, 6)),
b=copyOfRange(a, 5, 100),
x=sequence(100, 0, 1),
list(tuple(plot=line, x=x, y=a),
tuple(plot=line, x=x, y=b)))
- The let expression is setting variable a, b, x and returning a list of tuples with plotting data.
- Variable a holds the data for the first sine wave.
- Variable b has a copy of the array stored in variable a starting from index 5. Starting the second sine wave from the 5th index creates the lag time between the two sine waves.
- Variable x holds a sequence from 0 to 99 which will be used for plotting the x access.
- The list contains two output tuples which provide the plotting data. You'll notice that the syntax for plotting two lines does not involve the plot function, but instead requires a list of tuples containing plotting data. As Sunplot matures the syntax for plotting a single line and multiple lines will likely converge.
Convolution and Cross-correlation
We're going to be using the math behind convolution to cross-correlate the two waveforms. So before delving into cross-correlation its worth having a discussion about convolution.
Convolution is a mathematical operation that has a wide number of uses. In the field of Digital Signal Processing (DSP) convolution is considered the most important function. Convolution is also a key function in deep learning where it's used in convolutional neural networks.
So what is convolution? Convolution takes two waveforms and produces a third waveform through a mathematical operation. The gist of the operation is to reverse one of the waveforms and slide it across the other waveform. As the waveform is slid across the other, a cross product is calculated at each position. The integral of the cross product at each position is stored in a new array which is the "convolution" of the two waveforms.
That's all very interesting, but what does it have to do with cross-correlation? Well as it turns out convolution and cross-correlation are very closely related. The only difference between convolution and cross-correlation is that the waveform being slid across is not reversed.
In the example below the convolve function (conv) is called on two waveforms. Notice that the second waveform is reversed with the rev function before the convolution. This is done because the convolution operation will reverse the second waveform. Since it's already been reversed the convolution function will reverse it again and work with the original waveform.
This will result in a cross-correlation operation rather then convolution.
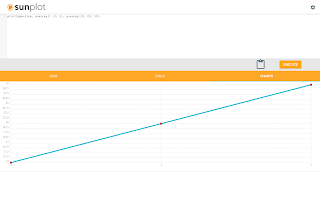
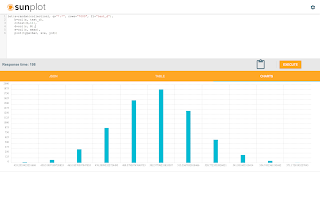
The screenshot below shows the cross-correlation operation and it's plot.
The highest peak in the cross-correlation plot is the point where the two waveforms have the highest correlation.
Finding the Delay Between Two Time Series
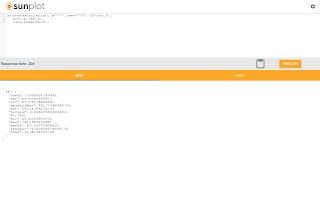
We've visualized the cross-correlation, but how do we use the cross-correlation array to find the delay? We actually have a function called finddelay which will calculate the delay for us. The finddelay function uses convolution math to calculate the cross-correlation array. But instead of returning the cross-correlation array it takes it a step further and calculates the delay.
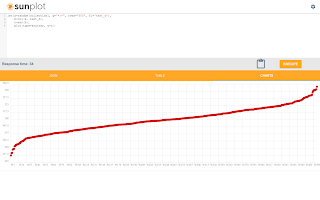
The screenshot below shows how the finddelay function is called.
Lagged Regression
Once we know the delay between the two sine waves it's very easy to perform the lagged regression. The screenshot below shows the statistical expression and regression result.
Let's quickly review the expression and interpret the regression results:
let(a=sin(sequence(100, 1, 6)),
b=copyOfRange(a, 5, 100),
c=finddelay(a, b),
d=copyOfRange(a, c, 100),
r=regress(b, d),
tuple(reg=r))
- Variables a and b hold the two sine waves with the 5 increment lag time between them.
- Variable c holds the delay between the two signals.
- Variable d is a copy of the first sine wave starting from the delay index specified in variable c.
The sine waves in variables b and d are now in sync and ready to regress.
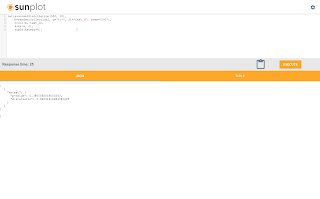
The regression result is as follows:
{ "reg": { "significance": 0, "totalSumSquares": 48.42686366058407, "R": 1, "meanSquareError": 0, "intercept": 0, "slopeConfidenceInterval": 0, "regressionSumSquares": 48.42686366058407, "slope": 1, "interceptStdErr": 0, "N": 95, "RSquare": 1 } }
The RSquare value of 1 indicates that the regression equation perfectly describes the linear relationship
between the two arrays.